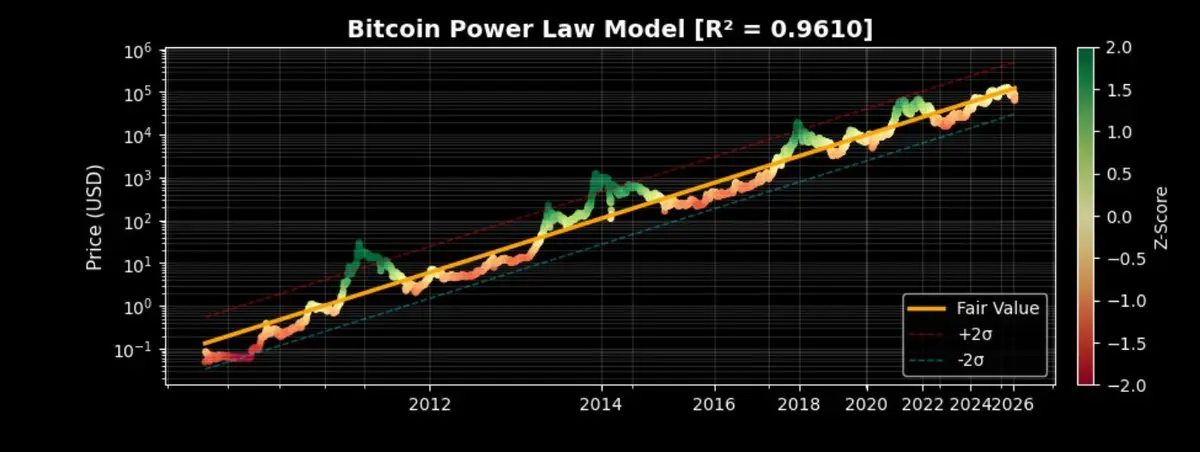
BTC_POWER_LA
用戶暫無簡介
BTC_POWER_LA
- 讚賞
- 點讚
- 留言
- 轉發
- 分享
- 讚賞
- 點讚
- 留言
- 轉發
- 分享
- 讚賞
- 1
- 1
- 轉發
- 分享
repanzal :
:
2026 GOGOGO 👊想像我們生活在一個模擬中,時間本身像比特幣的區塊時間一樣運作。
有一個宇宙共識過程,類似於工作量證明,只有當某個程序成功並且“挖出”一個區塊時,時鐘才會“滴答”一次。在這個畫面中,現實以離散的步伐前進,一次一個區塊。
但這實際上並沒有解決與時間相關的任何概念謎題。工作量證明過程、導致區塊產生的因果互動,以及執行該計算所需的物理步驟,仍然必須在連續時間中展開,並且在區塊鏈之外。你只是將問題向上移了一個層次。
如果你又引入另一個“區塊鏈宇宙”來調節這些過程的時間,你就創造了一個無限倒退的循環。沒有任何解釋;問題只是被推遲。到那時,解釋就崩潰成經典的宇宙學非答案:它全是烏龜一直往下的故事。
所以即使在這個假設的區塊時間宇宙中,你也沒有解釋時間——你只是用不同的協議包裝了它。
有一個宇宙共識過程,類似於工作量證明,只有當某個程序成功並且“挖出”一個區塊時,時鐘才會“滴答”一次。在這個畫面中,現實以離散的步伐前進,一次一個區塊。
但這實際上並沒有解決與時間相關的任何概念謎題。工作量證明過程、導致區塊產生的因果互動,以及執行該計算所需的物理步驟,仍然必須在連續時間中展開,並且在區塊鏈之外。你只是將問題向上移了一個層次。
如果你又引入另一個“區塊鏈宇宙”來調節這些過程的時間,你就創造了一個無限倒退的循環。沒有任何解釋;問題只是被推遲。到那時,解釋就崩潰成經典的宇宙學非答案:它全是烏龜一直往下的故事。
所以即使在這個假設的區塊時間宇宙中,你也沒有解釋時間——你只是用不同的協議包裝了它。
BTC-0.76%

- 讚賞
- 1
- 1
- 轉發
- 分享
repanzal :
:
2026 GOGOGO 👊好的,我沒有花太長時間就發現這篇論文非常“業餘”。我支持將比特幣與物理學(聯繫起來的想法,這是我已經做了12年的事情),但必須用一種對其他物理學家來說有效且易於理解的方法來進行。
這篇論文中的主張大多不成立(,從核心命題開始)。
以下是論文主旨的主要問題點分析:
這是一個雄心勃勃、修辭強烈的摘要——但它將敏銳的直覺與幾個草率的類別錯誤、過度聲稱和弱類比混為一談。我將拆解主要的弱點,以及它們從物理學+科學哲學角度為何具有問題。
1) 類別錯誤:比特幣時間 ≠ 物理時間
“比特幣是歷史上第一個我們可以實證觀察到量化時間長什麼樣的系統,而它並非由時間本身構成。”
這是核心錯誤。
比特幣的區塊時間是:
一個人為設計的協議時鐘
運行在物理硬體上
嵌入在真實的物理時間中
受到延遲、抖動、時鐘漂移、網路延遲的影響
它並非“在”物理時間之外。
它是一個在連續物理時間內實現的派生離散計數器。
你不是在觀察“量子化的時間”。
你是在觀察一個在連續物理時間中演化的計算系統的離散狀態轉換。
這等同於說:
“CPU時鐘告訴我們量子化時間的樣子。”
這是錯的。CPU時鐘是一個在類比物理上實現的數字抽象。
因此這個類比:
❌ 混淆了離散計數器與本體論上的時間
❌ 將協議離散化誤認為物理量子化
❌ 犯下了表徵謬誤
2) 錯
查看原文這篇論文中的主張大多不成立(,從核心命題開始)。
以下是論文主旨的主要問題點分析:
這是一個雄心勃勃、修辭強烈的摘要——但它將敏銳的直覺與幾個草率的類別錯誤、過度聲稱和弱類比混為一談。我將拆解主要的弱點,以及它們從物理學+科學哲學角度為何具有問題。
1) 類別錯誤:比特幣時間 ≠ 物理時間
“比特幣是歷史上第一個我們可以實證觀察到量化時間長什麼樣的系統,而它並非由時間本身構成。”
這是核心錯誤。
比特幣的區塊時間是:
一個人為設計的協議時鐘
運行在物理硬體上
嵌入在真實的物理時間中
受到延遲、抖動、時鐘漂移、網路延遲的影響
它並非“在”物理時間之外。
它是一個在連續物理時間內實現的派生離散計數器。
你不是在觀察“量子化的時間”。
你是在觀察一個在連續物理時間中演化的計算系統的離散狀態轉換。
這等同於說:
“CPU時鐘告訴我們量子化時間的樣子。”
這是錯的。CPU時鐘是一個在類比物理上實現的數字抽象。
因此這個類比:
❌ 混淆了離散計數器與本體論上的時間
❌ 將協議離散化誤認為物理量子化
❌ 犯下了表徵謬誤
2) 錯
- 讚賞
- 點讚
- 留言
- 轉發
- 分享
為什麼在人工智慧中如此多的龍蝦引用?
Accelerando 是一本接近未來到後奇點的科幻小說,描述一個家庭的三代人在從晚期資本主義轉變為由人工智慧、上傳技術和機器經濟主導的徹底變革後的人類文明。這部小說以一系列相互連結的故事結構呈現,追蹤科技變革的加速——快到人類的制度、價值觀甚至生物認知都難以跟上。
其中一個早期且令人難忘的元素是升級的龍蝦出現。這些是真實的甲殼類動物,其神經系統被先進技術掃描、建模並部分模擬。通過這個過程,龍蝦——通常是簡單的生物體——被有效地轉變為具有感知或半感知能力的數字實體,能夠參與經濟和信息系統。它們成為故事中新興後人類生態系統中次要但象徵意義深遠的角色。
查看原文Accelerando 是一本接近未來到後奇點的科幻小說,描述一個家庭的三代人在從晚期資本主義轉變為由人工智慧、上傳技術和機器經濟主導的徹底變革後的人類文明。這部小說以一系列相互連結的故事結構呈現,追蹤科技變革的加速——快到人類的制度、價值觀甚至生物認知都難以跟上。
其中一個早期且令人難忘的元素是升級的龍蝦出現。這些是真實的甲殼類動物,其神經系統被先進技術掃描、建模並部分模擬。通過這個過程,龍蝦——通常是簡單的生物體——被有效地轉變為具有感知或半感知能力的數字實體,能夠參與經濟和信息系統。它們成為故事中新興後人類生態系統中次要但象徵意義深遠的角色。

- 讚賞
- 1
- 1
- 轉發
- 分享
repanzal :
:
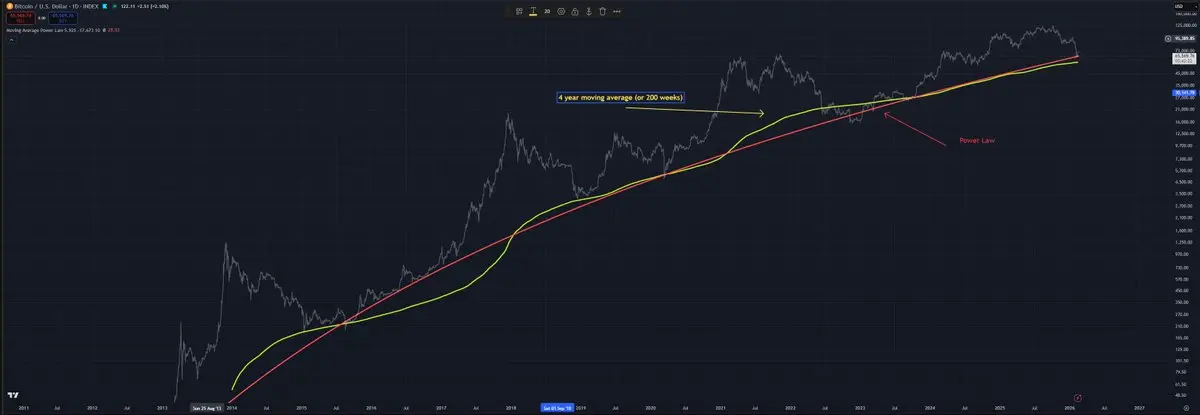
2026 GOGOGO 👊許多人將200週移動平均線視為某種強大的預測指標。事實上,它本身並沒有內在的預測能力。 它真正做的是揭示已經存在的潛在結構。 比特幣遵循長期的冪律增長。如果你將比特幣的價格在大約四年的窗口內(~208週)進行平均,你實際上是在平滑圍繞該結構性趨勢的短期振盪。偏離冪律的部分會被抑制,長期的模式變得更為清晰。這就是為什麼200週MA“有效”——不是因為平均值具有魔力,而是因為比特幣本身具有強烈的潛在縮放定律。 平均值並不創造結構。它們只是在結構已存在的情況下揭示它。 如果比特幣沒有遵循一個穩定的長期縮放關係,200週平均值看起來就不會特別有意義,也不會顯得像一個“支撐”水平。因此,200週MA的表現力是對潛在冪律行為韌性的反映,而不是移動平均本身的屬性。 換句話說:移動平均是描述性的,而非因果性的。 它們可以揭示現有的規律,或顯示根本不存在規律——但它們本身並不產生預測性。
BTC-0.76%
- 讚賞
- 2
- 2
- 轉發
- 分享
repanzal :
:
Ape In 🚀查看更多
在太平洋標準時間晚上7:00,我們將迎來《比特幣的物理學》長時間休息後的新一集。
我們將討論新成立的科學比特幣研究所以及以下議程。
節目將在X、YouTube和Twitch上播出。
連結在留言中。
我們將討論新成立的科學比特幣研究所以及以下議程。
節目將在X、YouTube和Twitch上播出。
連結在留言中。
BTC-0.76%
- 讚賞
- 1
- 1
- 轉發
- 分享
repanzal :
:
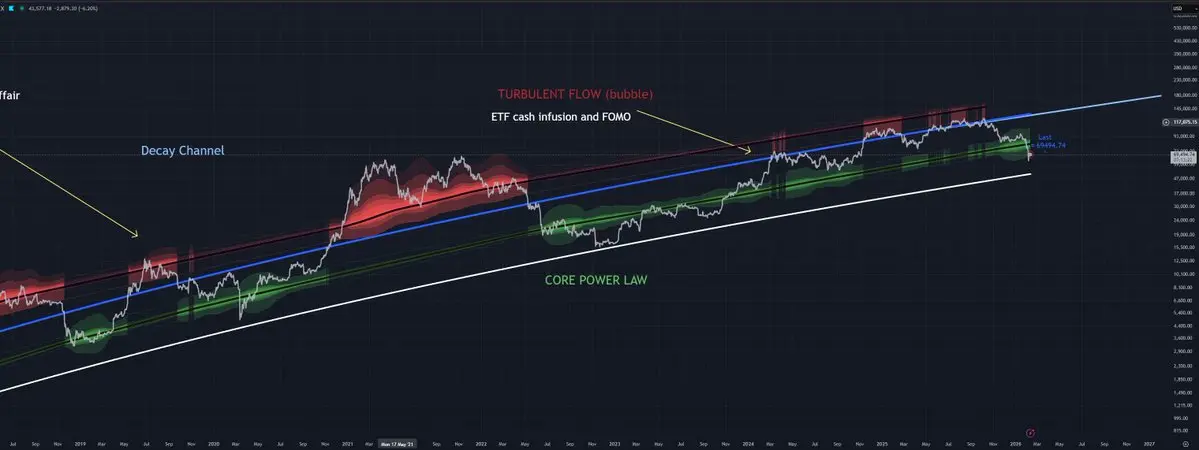
2026 GOGOGO 👊幂律比以往任何時候都更強大。
事實上,我們從未進入過湍流流動 (紅色區域),這使得幂律在統計上比以往周期更為穩健。我們多次試圖推進到湍流流動 (自2025年11月起的紅色暗示),但每次價格都回到綠色區域。之後,我們花了數月時間在幂律周圍振盪——基本上是2026年的大部分時間。
即使價格跌破藍色參考線,11月至1月底的增長率仍與幂律平行。換句話說,我們在水平上偏離,而非斜率上偏離。
關鍵是,支撐幂律從未被突破——甚至在最近的嚴重崩盤期間也沒有。
看看圖表:這是最能解釋數據的模型。
我們現在又回到了核心幂律範圍內,Bitcoin歷史上大部分時間都在這個範圍內 (大約每4年周期中的2年)。問題是,這個模式是否也會在接下來的兩年內重演。
即使在最近的嚴重崩盤期間,我們也沒有突破支撐線。
事實上,我們從未進入過湍流流動 (紅色區域),這使得幂律在統計上比以往周期更為穩健。我們多次試圖推進到湍流流動 (自2025年11月起的紅色暗示),但每次價格都回到綠色區域。之後,我們花了數月時間在幂律周圍振盪——基本上是2026年的大部分時間。
即使價格跌破藍色參考線,11月至1月底的增長率仍與幂律平行。換句話說,我們在水平上偏離,而非斜率上偏離。
關鍵是,支撐幂律從未被突破——甚至在最近的嚴重崩盤期間也沒有。
看看圖表:這是最能解釋數據的模型。
我們現在又回到了核心幂律範圍內,Bitcoin歷史上大部分時間都在這個範圍內 (大約每4年周期中的2年)。問題是,這個模式是否也會在接下來的兩年內重演。
即使在最近的嚴重崩盤期間,我們也沒有突破支撐線。
BTC-0.76%
- 讚賞
- 點讚
- 留言
- 轉發
- 分享
- 讚賞
- 點讚
- 留言
- 轉發
- 分享
看看長期趨勢。仍在路上,持續向前。
查看原文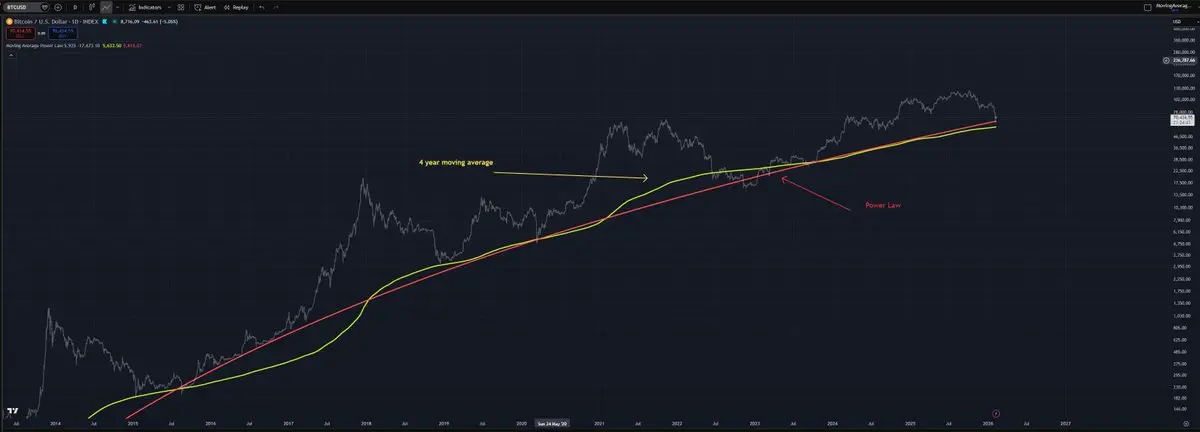
- 讚賞
- 點讚
- 留言
- 轉發
- 分享
熱門話題
查看更多17.69萬 熱度
3.69萬 熱度
3.43萬 熱度
7.76萬 熱度
1.59萬 熱度
熱門 Gate Fun
查看更多- 市值:$2475.86持有人數:10.00%
- 市值:$2540.05持有人數:20.21%
- 市值:$0.1持有人數:10.00%
- 市值:$2472.41持有人數:10.00%
- 市值:$2502.4持有人數:20.00%
置頂
福利加碼,Gate 廣場明星帶單交易員二期招募開啟!
入駐發帖 · 瓜分 $20,000 月度獎池 & 千萬級流量扶持!
如何參與:
1️⃣ 報名成為跟單交易員:https://www.gate.com/copytrading/lead-trader-registration/futures
2️⃣ 報名活動:https://www.gate.com/questionnaire/7355
3️⃣ 入駐 Gate 廣場,持續發布交易相關原創內容
豐厚獎勵等你拿:
首帖福利:首發優質內容即得 $30 跟單体验金
雙周內容激勵:每雙周瓜分 $500U 內容獎池
排行榜獎勵:Top 10 交易員額外瓜分 $20,000 登榜獎池
流量扶持:精選帖推流、首頁推薦、周度明星交易員曝光
活動時間:2026 年 2 月 12 日 18:00 – 2 月 24 日 24:00(UTC+8)
詳情:https://www.gate.com/announcements/article/49849Gate 廣場內容挖礦獎勵繼續升級!無論您是創作者還是用戶,挖礦新人還是頭部作者都能贏取好禮獲得大獎。現在就進入廣場探索吧!
創作者享受最高60%創作返佣
創作者獎勵加碼1500USDT:更多新人作者能瓜分獎池!
觀眾點擊交易組件交易贏大禮!最高50GT等新春壕禮等你拿!
詳情:https://www.gate.com/announcements/article/49802🏮 新年快樂,馬上發財!Gate 廣場 $50,000 紅包雨狂降!
發帖即領,手慢無 👉 https://www.gate.com/campaigns/4044
🧨 三重驚喜,陪您紅火過新年:
1️⃣ $50,000 紅包雨:發帖即領,新用戶 100% 中獎,單帖最高 28 GT
2️⃣ 馬年錦鯉:帶 #我在Gate广场过新年 發帖,抽 1 人送 50 GT + 新春禮盒
3️⃣ 創作者榜單賽:贏國米球衣、Red Bull 聯名夾克、VIP 露營套裝等豪禮
📅 2/9 17:00 – 2/23 24:00(UTC+8)
請將 App 更新至 8.8.0+ 版本參與
詳情:https://www.gate.com/announcements/article/49773Gate 廣場“新星計劃”正式上線!
開啟加密創作之旅,瓜分月度 $10,000 獎勵!
參與資格:從未在 Gate 廣場發帖,或連續 7 天未發帖的創作者
立即報名:https://www.gate.com/questionnaire/7396
您將獲得:
💰 1,000 USDT 月度創作獎池 + 首帖 $50 倉位體驗券
🔥 半月度「爆款王」:Gate 50U 精美周邊
⭐ 月度前 10「新星英雄榜」+ 粉絲達標榜單 + 精選帖曝光扶持
加入 Gate 廣場,贏獎勵 ,拿流量,建立個人影響力!
詳情:https://www.gate.com/announcements/article/49672